With the latest software release, it’s now much easier to create and manage calibrations. We can go even further and start to take advantage of all the data you are generating to improve individual calibrations in your cluster. Let’s see how.
In the before times…
Previously, calibration curves were created per Pioreactor. That is, the Pioreactor i would generate the data, D_i, and the software would create a calibration curve from D_i. You would do this for each N Pioreactor in your cluster, inferring calibration curves as polynomials, p_i(x | D_i).
This works, but you aren’t taking advantage of all the data at your disposal. What do I mean by that? Each Pioreactor is pretty similar to each other, so we should be able to “borrow” information from one Pioreactor’s calibration to help inference on another’s. This is called hierarchical regression, where there are two inferences being done: one at a group level (“all pioreactors”), and one at the individual level (“each pioreactor”). In the extreme limit, you can have a individual with very sparse data (even no data!), still include it in the regression, and it gets the inference benefits from all the data.
In practice, we’ll have the leader pull calibration data from each worker, perform a hierarchical regression on all the data, and create new calibrations on each worker.
The model
Let p(x) = w_dx^d + ... + w_0 be a polynomial with currently unknown coefficients. This polynomial is to be shared between all N Pioreactors (group level regression). Let A_i be (unknown) Pioreactor-specific scalar values. Then p_i(x) = A_i p(x) is Pioreactor i's calibration curve.
This simple model has the advantage of being scalable to many Pioreactors: we only need to estimate n + (d + 1) parameters. Other models we considered scaled like n d, which is totally prohibitive.
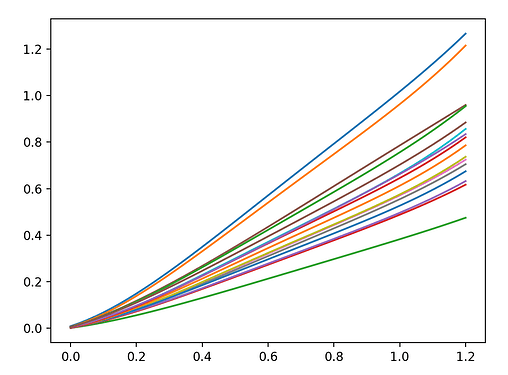
And in practice, we do see this functional form in cluster’s calibrations. For example, below are 4-degree OD calibration curves from a user’s 16 worker cluster:
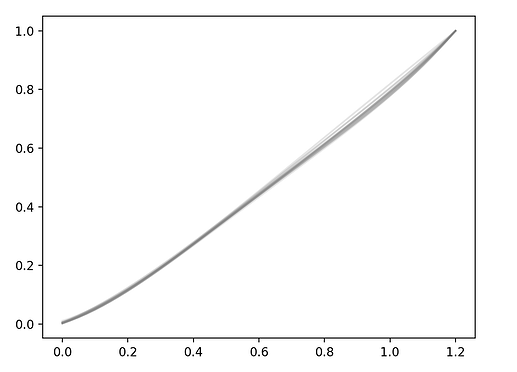
They don’t look very similar, but if scale each curve by its max (normalizing it to be between 0 and 1) and then replot:
There’s still some variability, but it’s very minor. This chart suggests that our simple model will be sufficient to capture both the similarities and differences between Pioreactors’ calibrations (and if not, just create subgroups of Pioreactors, and do the same inference on each subgroup).
There’s one more feature I want to bring up, and this is probably the most useful feature. It’s the idea of shrinkage. Shrinkage is a general term to describe regression-to-the-mean: it’s a statistical way to say “yea you got a high score, but you got lucky - try doing it again”. That is, data that is far away from an average, probably got there in-part by chance. This has applications: imagine a room full of University students doing calibrations: untrusted, sticky, and distracted, their calibrations will be much more noisy, and some will look more extreme due to this. However, there is still information in each calibration, so we still use them all in the final model. But we strongly shrink the A_i terms toward each other (actually, we shrink them towards the value 1) - more extreme values are shrunk more. On the other hand, imagine a mature post-doc doing calibrations: highly trusted, excellent techniques: we might not need to shrink their estimates much.
We include a parameter in the model, called \lambda_A, that control how much we should shrink the estimates.
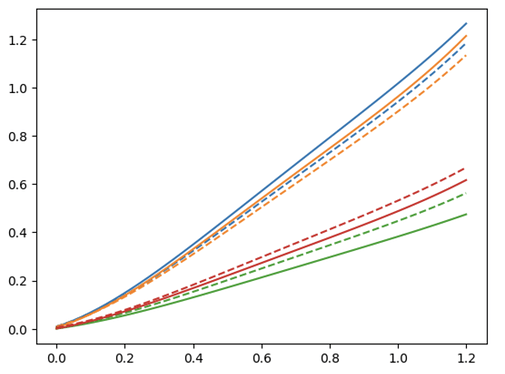
Let’s see this in practice. Below, I’ve plotted four original calibrations in solid lines, and four “regressed and shrunk” calibrations in dashed lines.
As you can see, the new calibrations are slightly closer to each other than the originals. The curves are also adequately modelled.
You might be thinking: “this is crazy: shifting curves based on other Pioreactors!” But it’s not, it’s actually crazy not to do this. Consider the green curve. All the other curves are above it - do you really think that green curve shouldn’t be just a little higher? Don’t you think something external to your data collection might have pulled that data just a tad lower than it should have been? Still not convinced? Go pick up a book on Bayesian inference.
Plugin installation and usage
So we’ve explored the model, how do we actually do this? The new plugin pioreactor-calibration-shrinkage (details here) can be installed on your leader. You can run it with:
pio calibrations shrinkage --device
Next, you’ll select calibrations from your workers to include in your regression. And after providing some options, the program will run the regression and show you the output. If you’re happy, you can save the results and create new calibrations on each worker.
The plugin is a bit “raw” right now (I like it, but I developed it and can read statistical output), so feel free to try it and let me know what you think!